문제
스도쿠는 18세기 스위스 수학자가 만든 '라틴 사각형'이랑 퍼즐에서 유래한 것으로 현재 많은 인기를 누리고 있다. 이 게임은 아래 그림과 같이 가로, 세로 각각 9개씩 총 81개의 작은 칸으로 이루어진 정사각형 판 위에서 이뤄지는데, 게임 시작 전 일부 칸에는 1부터 9까지의 숫자 중 하나가 쓰여 있다.

나머지 빈 칸을 채우는 방식은 다음과 같다.
- 각각의 가로줄과 세로줄에는 1부터 9까지의 숫자가 한 번씩만 나타나야 한다.
- 굵은 선으로 구분되어 있는 3x3 정사각형 안에도 1부터 9까지의 숫자가 한 번씩만 나타나야 한다.
위의 예의 경우, 첫째 줄에는 1을 제외한 나머지 2부터 9까지의 숫자들이 이미 나타나 있으므로 첫째 줄 빈칸에는 1이 들어가야 한다.

또한 위쪽 가운데 위치한 3x3 정사각형의 경우에는 3을 제외한 나머지 숫자들이 이미 쓰여있으므로 가운데 빈 칸에는 3이 들어가야 한다.
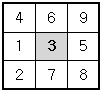
이와 같이 빈 칸을 차례로 채워 가면 다음과 같은 최종 결과를 얻을 수 있다.

게임 시작 전 스도쿠 판에 쓰여 있는 숫자들의 정보가 주어질 때 모든 빈 칸이 채워진 최종 모습을 출력하는 프로그램을 작성하시오.
입력
아홉 줄에 걸쳐 한 줄에 9개씩 게임 시작 전 스도쿠판 각 줄에 쓰여 있는 숫자가 한 칸씩 띄워서 차례로 주어진다. 스도쿠 판의 빈 칸의 경우에는 0이 주어진다. 스도쿠 판을 규칙대로 채울 수 없는 경우의 입력은 주어지지 않는다.
출력
모든 빈 칸이 채워진 스도쿠 판의 최종 모습을 아홉 줄에 걸쳐 한 줄에 9개씩 한 칸씩 띄워서 출력한다.
스도쿠 판을 채우는 방법이 여럿인 경우는 그 중 하나만을 출력한다.
접근
각 칸에 대하여 해당 칸에 들어갈 수 있는 숫자를 확인하고, 그 중 하나를 입력한 후 다음 칸을 탐색한다. 탐색 중에 칸을 채울 수 있는 숫자가 없을 경우 되돌아가 다음 숫자를 선택하여 채우는 백트래킹 문제이다.
스도쿠의 칸에 들어갈 수 있는 수는 1부터 9까지 총 9개이고 그 칸에 들어갈 수 있는 숫자는 가로 방향으로 겹쳐서도 안되고, 세로 방향으로도, 그리고 해당 칸이 포함된 3*3 칸에도 겹치면 안된다. 빈칸에 들어갈 수 있는 숫자가 무엇인지 찾는 함수와 각 칸에 대하여 백트래킹 방식으로 탐색하는 함수를 이용하였고, 모든 칸이 채워지면 해당 값을 출력하여 답을 구할 수 있다.
코드
import sys
sudoku = []
for i in range(9):
a = list(map(int, sys.stdin.readline().split()))
sudoku.append(a)
zeros = [(i, j) for i in range(9) for j in range(9) if sudoku[i][j] == 0] # 값이 0인 곳, 즉 빈칸을 요소로 갖는 list
ans = False
def check(i, j): # (i, j)가 주어졌을 때 해당 칸에 들어갈 수 있는 숫자가 무엇인지 찾는 함수
pool = [i for i in range(1, 10)]
for k in range(9):
if sudoku[i][k] in pool:
pool.remove(sudoku[i][k])
if sudoku[k][j] in pool:
pool.remove(sudoku[k][j])
i //= 3
j //= 3
for p in range(i * 3, (i + 1) * 3):
for q in range(j * 3, (j + 1) * 3):
if sudoku[p][q] in pool:
pool.remove(sudoku[p][q])
return pool
def solve_sudoku(x):
global ans
if ans:
return
if x == len(zeros): # 모든 칸이 채워졌을 때 결과 출력
for row in sudoku:
print(*row)
ans = True
return
else:
(i, j) = zeros[x]
possible = check(i, j)
for num in possible:
sudoku[i][j] = num # 탐색중인 칸에 들어갈 수 있는 숫자 중 하나를 대입 후 다음 칸 탐색
solve_sudoku(x + 1)
sudoku[i][j] = 0
solve_sudoku(0)더 생각해 볼 것?
...
'코딩 > 백준 (Python)' 카테고리의 다른 글
| 백준 1003번: 피보나치 함수 (Python) (0) | 2021.03.26 |
|---|---|
| 백준 14888번: 연산자 끼워넣기 (Python, PyPy3) (0) | 2021.03.26 |
| 백준 9663번: N-Queen (Python, PyPy3) (0) | 2021.03.26 |
| 백준 1436번: 영화감독 숌 (Python) (0) | 2021.03.25 |
| 백준 1018번: 체스판 다시 칠하기 (Python) (0) | 2021.03.25 |




최근댓글