
Strongly Connected Component(SCC) 문제를 푸는 방법에는 크게 Kosaraju 알고리즘과 Tarjan 알고리즘이 있다. 두가지 알고리즘으로 푸는데 매우 헤매었기 때문에 시간을 조금 들여서라도 두가지 모두 정리하고 코드를 자세하게 주석을 달아 설명해두고 넘어가려고 한다.
접근 (Kosaraju)
코사라주 알고리즘을 수행하기 위해서는 먼저 문제에 주어진 정방향 그래프와, 각 그래프의 방향이 정반대인 역방향 그래프 두가지를 준비해야한다.
먼저 정방향 그래프를 이용하여 모든 그래프 상에서 dfs 탐색을 수행하고, dfs 탐색이 종료되는 순서대로 stack에 append 해준다. 이후 해당 stack에서 요소들을 한개씩 pop하여 순서대로 역방향 dfs를 수행하고, 한번 수행에 탐색되는 모든 정점들을 SCC로 묶는다. 스택이 빌 때까지 이 작업을 계속해주면 SCC를 구할 수 있다.
예제 문제를 그림으로 다음과 같이 표현할 수 있다.

1번 노드에서 부터 시작하여 dfs 알고리즘으로 탐색해나간다면 가장 먼저 5에서 진행할 수 있는 노드가 없어 dfs 가 종료되게 된다. 따라서 5와 4의 순서대로 스택에 쌓이게 된다.

마찬가지로 dfs 탐색을 계속해나아간다면 아래와 같은 stack을 구할 수 있다.

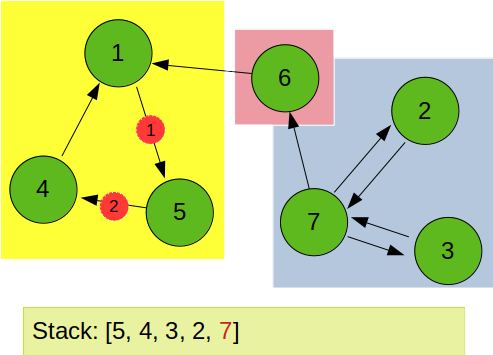
이후 역방향 그래프를 이용하여 stack 에서 pop 되는 요소 순서대로 역방향 dfs 를 진행하게 된다. 아래 그림과 같이 stack 에서 가장 먼저 1번 노드가 pop 되게 된다.

1번 노드에서 역방향 dfs 를 진행하면 5를 통해 4로 진행하여 1, 5, 4 가 한개의 SCC 로 묶임을 알 수 있다.

다음으로 pop 되는 6번 노드에서는 진행할 수 있는 노드가 없으므로 한개의 노드가 SCC 를 이루게 된다.

마지막으로 7에서 시작하는 역방향 dfs를 통해 7, 2, 3이 한개의 SCC로 묶이게 된다.
코드
import sys
sys.setrecursionlimit(10 ** 6)
v, e = map(int, sys.stdin.readline().split())
graph = [[] for _ in range(v + 1)]
reverse_graph = [[] for _ in range(v + 1)]
for _ in range(e):
a, b = map(int, sys.stdin.readline().split())
# 정방향 그래프 및 역방향 그래프에 주어진 그래프를 추가해준다.
graph[a].append(b)
reverse_graph[b].append(a)
# 정방향 dfs, dfs 가 종료되는 노드를 stack 에 쌓는다.
def dfs(node, visited, stack):
visited[node] = 1
for ne in graph[node]:
if visited[ne] == 0:
dfs(ne, visited, stack)
stack.append(node)
# 역방향 dfs, 탐색하는 순서대로 stack (scc) 에 쌓는다.
def reverse_dfs(node, visited, stack):
visited[node] = 1
stack.append(node)
for ne in reverse_graph[node]:
if visited[ne] == 0:
reverse_dfs(ne, visited, stack)
stack = []
visited = [0] * (v + 1)
# 모든 노드에서 정방향 dfs 를 수행한다.
for i in range(1, v + 1):
if visited[i] == 0:
dfs(i, visited, stack)
visited = [0] * (v + 1)
result = []
# 스택이 빌 때까지 pop 되는 요소에서 역방향 dfs 를 진행하여 scc 를 결과에 추가해준다.
while stack:
ssc = []
node = stack.pop()
if visited[node] == 0:
reverse_dfs(node, visited, ssc)
result.append(sorted(ssc))
print(len(result))
results = sorted(result)
for i in results:
print(*i, -1)접근 (Tarjan)
타잔 알고리즘을 이해하고 코딩하기가 매우 어려웠다. 타잔 알고리즘은 코사라주와는 달리 한번의 dfs 로 SCC를 구할 수 있다. 하지만 백준 2150번 문제 기준 두가지 방법에 시간 차이는 없었다. 그래프를 dfs 탐색하면서 각 노드에 id 와 low 를 지정한다. 그리고 다음 노드의 low 와 현재 노드의 low 를 비교하여 더 작은 수로 갱신해주고, 최종적으로는 같은 low 값을 가지고 있는 노드들끼리 같은 SCC 로 묶어주게 된다.
예제 문제를 그림으로 표현하면 아래와 같다. 먼저 노드의 id 와 low 를 표시하기 위한 방법을 아래와 같이 표시하겠다.
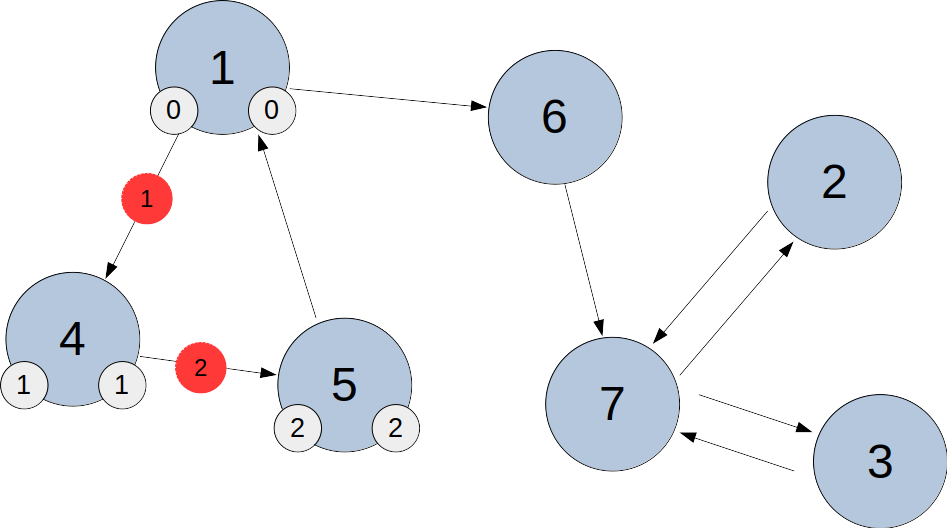
1번 노드에 id, low 를 0 지정, 탐색 순서대로 4와 5번 노드에 각각 1과 2를 지정해준다.
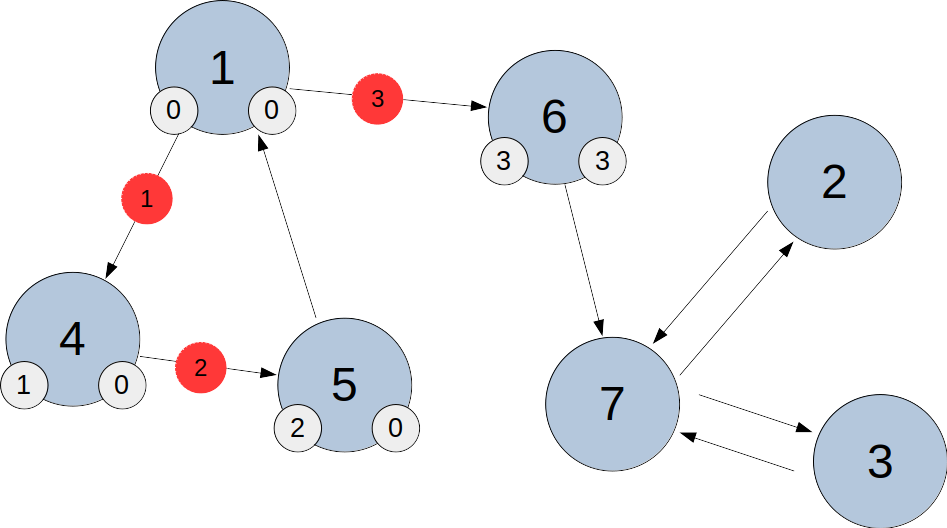
5번 노드에 도달했을 때, 5번 노드의 다음 노드는 1이고 1의 low 값은 0이기 때문에 5번 노드의 low 값을 0으로 갱신해준다.

마찬가지로 dfs 완료 순서에 따라 4번 노드도 5번 노드와 비교하여 low 값을 0으로 갱신해준다.

1번 노드에서 다음 순서인 6번 노드에 3을 지정해준다.
마찬가지로 7번 이후 노드들을 탐색하면 아래와 같이 low 값을 갱신해줄 수 있고, 같은 low 값을 가지고 있는 노드들 끼리 SCC 관계를 가지게 된다. 즉 위의 코사라주 알고리즘과 동일하게 [1, 4, 5], [6], [2, 3, 7] 총 3개의 SCC 를 가진다.

코드
import sys
sys.setrecursionlimit(10 ** 6)
v, e = map(int, sys.stdin.readline().split())
graph = [[] for _ in range(v + 1)]
for _ in range(e):
a, b = map(int, sys.stdin.readline().split())
graph[a].append(b)
stack = []
low = [-1] * (v + 1)
ids = [-1] * (v + 1)
visited = [0] * (v + 1)
idid = 0
result = []
def dfs(x, low, ids, visited, stack):
global idid
ids[x] = idid
low[x] = idid
idid += 1
visited[x] = 1
stack.append(x)
for ne in graph[x]:
if ids[ne] == -1:
dfs(ne, low, ids, visited, stack)
low[x] = min(low[x], low[ne])
elif visited[ne] == 1:
low[x] = min(low[x], ids[ne])
w = -1
scc = []
if low[x] == ids[x]:
while w != x:
w = stack.pop()
scc.append(w)
visited[w] = -1
result.append(sorted(scc))
for i in range(1, v + 1):
if ids[i] == -1:
dfs(i, low, ids, visited, stack)
print(len(result))
for i in sorted(result):
print(*i, -1)더 생각해 볼 것?
...
코드나 내용 관련 조언, 부족한 점 및 질문 언제든 환영합니다!
'코딩 > 백준 (Python)' 카테고리의 다른 글
| 백준 3977번: 축구 전술 (Python) (0) | 2021.07.11 |
|---|---|
| 백준 4196번: 도미노 (Python) (0) | 2021.07.11 |
| 백준 13511번: 트리와 쿼리 2 (Python) (0) | 2021.07.03 |
| 백준 3176번: 도로 네트워크 (Python, PyPy3) (0) | 2021.07.02 |
| 백준 11438번: LCA 2 (Python, PyPy3) (0) | 2021.06.29 |




최근댓글