
접근
힙 트리(heap tree)란 여러 개의 값 중에서 가장 크거나 작은 값을 빠르게 찾기 위해 만든 이진 트리이다.

힙에는 가장 큰 값을 구하기 위한 최대 힙과, 가장 작은 값을 구하기 위한 최소 힙이 있으며, 공통적으로 힙은 항상 완전 이진 트리(트리의 위부터 아래, 왼쪽에서 오른쪽 순서로 빠짐 없이 채워져 있는 트리)의 형태를 가지고 있어야 한다. 최대 힙은 부모의 값은 항상 자식들의 값보다 크거나 같아야 하고, 최소 힙은 부모의 값이 항상 자식보다 작거나 같아서, 이진 트리의 최대값, 혹은 최소 값을 구할 때 힙의 첫번째 요소를 통해 바로 구할 수 있게 된다.
이 문제에서는 최대 힙을 사용하여 문제를 풀며, 힙의 경우에는 python에 heapq 라이브러리가 있지만 원리를 제대로 다시 이해하기 위해 힙에 요소를 추가하고 제거하는 함수를 작성하였다.
최대 힙에서 새로운 요소를 추가할 경우 마지막에 요소를 넣고, 위쪽으로 부모 노드를 탐색하면서 추가된 요소가 부모 노드의 값보다 클 경우 자리를 바꿔나간다.

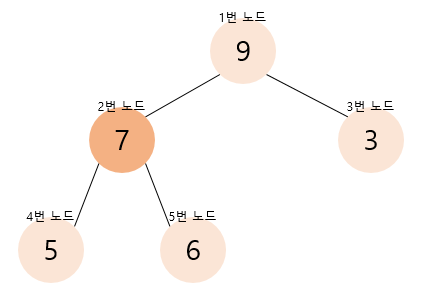
7의 값을 가진 새로운 노드가 추가되었을 때 이 노드의 부모노드인 2번노드와 비교하여 자식 노드의 값이 크기 때문에 위치를 서로 바꿔준다. 새로운 2번 노드와 그 부모 노드인 1번 노드를 비교하였을 때 부모노드가 크기 때문에 탐색은 종료되고 새로운 힙이 완성된다.
최대값을 구하고 그 트리에서 제거할 때는 힙 트리의 가장 마지막 값을 최대값이 있던 1번 요소에 넣고, 자식 노드들을 비교해나가면서 더 큰 자식 노드와 자리를 바꾼다.



마지막 노드인 5번 노드가 1번 노드로 이동하고, 1번 노드의 두 자식 노드인 2, 3번 노드와 비교하여 더 큰 값인 2번 노드와 자리를 교체한다. 바뀌고 난 후에 2번 노드와 그 자식 노드를 비교했을 때 자식 노드들보다 그 값이 크므로 힙이 완성되고 탐색이 종료된다.
힙은 한개의 리스트로 표현할 수 있는데, 이때 i번 노드가 부모 노드일 때, 그 자식노드들은 각각 2 * i번, 2 * i + 1번 순서를 가지게 되고, 이를 이용해 일반식을 구할 수 있다. 예를 들어 위의 예시에서 5번 노드를 추가할 때는 5 // 2 = 2 수식을 통하여 부모노드인 2번노드를 찾아 값을 비교할 수 있다.
코드
import sys
def heapappend(heap, num):
heap.append(num)
i = len(heap) - 1
while i > 1:
if heap[i] > heap[i // 2]:
tmp = heap[i]
heap[i] = heap[i // 2]
heap[i // 2] = tmp
i = i // 2
else:
break
def heappop(heap):
popvalue = heap[1]
tmp = heap.pop()
parent = 1
child = 2
while child <= len(heap) - 1:
if child < len(heap) - 1 and heap[child] < heap[child + 1]:
child += 1
if heap[child] <= tmp:
break
heap[parent] = heap[child]
parent = child
child *= 2
if len(heap) != 1:
heap[parent] = tmp
return popvalue
n = int(sys.stdin.readline())
a = [0]
for _ in range(n):
m = int(sys.stdin.readline())
if m == 0:
if len(a) == 1:
print(0)
else:
print(heappop(a))
else:
heapappend(a, m)더 생각해 볼 것?
...
코드나 내용 관련 조언, 부족한 점 및 질문 언제든 환영합니다!
'코딩 > 백준 (Python)' 카테고리의 다른 글
| 백준 11286번: 절댓값 힙 (Python) (0) | 2021.04.05 |
|---|---|
| 백준 1927번: 최소 힙 (Python) (0) | 2021.04.05 |
| 백준 12015번: 가장 긴 증가하는 부분 수열 2 (Python) (0) | 2021.04.05 |
| 백준 1300번: K번째 수 (Python) (0) | 2021.04.05 |
| 백준 2110번: 공유기 설치 (Python) (0) | 2021.04.05 |




최근댓글